Excelで重回帰分析：データの関係性を解読する方法

Excelで重回帰分析は、複数の独立変数が従属変数に及ぼす影響を定量的に解析する手法です。本記事では、Excelを使用してデータの関係性を解読する方法を詳細に解説します。具体的には、データの入力から分析結果の解釈まで、一連の手順を段階的に紹介します。さらに、重回帰分析の結果を活用するための重要な指標である決定係数、回帰係数、p値についても解説します。

Excelのデータ分析ツールを活用することで、複雑なデータの関係性を簡単に把握できます。また、多重共線性の確認方法や、Excelでの重回帰分析の応用例（マーケティング、金融など）も紹介します。本記事を読むことで、データ分析の基本から応用まで、Excelを活用した重回帰分析の全貌を理解し、実践的な分析スキルを身につけることができるでしょう。

📖 目次

Excelと重回帰分析の概要

Excelは、データ分析に広く使用されるツールであり、重回帰分析を含むさまざまな統計的手法を簡単に実行できます。重回帰分析は、複数の独立変数が一つの従属変数に与える影響を調べる手法で、ビジネスや研究の場面でよく利用されます。Excelのデータ分析ツールを使用することで、高度な統計分析を実行しながら、結果を直感的に理解できるようになります。

Excelのデータ分析ツールは、標準的な機能に加えて、アドインとして追加することで使用できます。このツールを有効に設定することで、重回帰分析を始めとする多くの統計分析機能を利用することが可能になります。データの入力や設定、分析結果の解釈など、一連の手順を簡単に追うことができるため、初心者でも比較的簡単に分析を始めることができます。

重回帰分析の結果を解釈する際には、決定係数、回帰係数、p値などの指標が重要となります。これらの指標は、モデルの説明力や変数の有意性を示し、分析結果の信頼性を高めます。また、多重共線性の確認も重要なステップであり、独立変数間の相関が高すぎないかを検証することで、分析結果の精度を向上させることができます。

Excelを使用した重回帰分析は、マーケティング戦略の立案、金融リスクの評価、製品開発の最適化など、さまざまな分野で活用されています。これらの実践例を紹介することで、読者が自らの業務や研究に応用できる具体的な手法を学ぶことができます。また、LINEST関数や手動での回帰式の計算などの代替方法も紹介し、より柔軟なデータ分析を支援します。

データの準備と入力

Excelで重回帰分析を行うためには、まずデータを適切に準備し、入力することが重要です。データセットは、従属変数（分析の対象となる変数）と独立変数（従属変数に影響を与えると考えられる変数）から構成されます。例えば、マーケティングにおける製品の売上を予測する場合、売上額が従属変数となり、広告費、製品の価格、競合他社の状況などが独立変数となります。

データをExcelのワークシートに配置する際は、各列を独立変数、従属変数に割り当て、各行を個々の観測値として入力します。列のヘッダーには変数名を設定し、データは数値として正確に入力します。データの範囲や形式が適切であることを確認し、不足やエラーがないか検証することも忘れずに行いましょう。これにより、分析の精度と信頼性が向上します。

データ分析ツールの起動

Excelにおけるデータ分析ツールの起動は、重回帰分析を行う上で最初の重要なステップです。まず、Excelのメニューから「データ」タブを選択します。その中から「数据分析」（データ分析）のボタンをクリックします。このボタンが表示されない場合は、Excelのアドイン設定で「分析ツール」を有効にする必要があります。この設定を有効にすると、「データ分析」のオプションが表示され、そこから「重回帰」を選択できます。選択後、新たなウィンドウが開き、重回帰分析の設定が行えるようになります。このウィンドウでは、独立変数と従属変数の範囲を指定し、出力先を設定することで、分析を開始できます。

重回帰分析の選択

重回帰分析は、複数の独立変数が1つの従属変数に与える影響を分析する統計的手法です。Excelでは、この分析を簡単に実行することができるため、ビジネスや研究において広く利用されています。データ分析にはさまざまな手法がありますが、重回帰分析は特に、複雑なデータセットから有意な関係性を導き出すのに役立ちます。例えば、売上高を予測する際に、広告費、店舗の立地、季節などの要因がどのように影響するかを考察することが可能です。Excelのデータ分析ツールを使用することで、これらの変数間の関係性を具体的に数値化し、より詳細な分析を行うことができます。

重回帰分析の選択には、いくつかの理由があります。まず、複数の独立変数を同時に考慮できるため、より現実的なモデルを作成できます。また、決定係数（R²）や回帰係数、p値などの統計指標を使用することで、分析結果の信頼性を確認できます。さらに、Excelのデータ分析ツールは使い勝手が良いため、高度な統計知識がなくても比較的簡単に分析を行うことができます。これらの利点により、重回帰分析はデータ分析の重要な手法の一つとなっています。

ただし、重回帰分析には注意点もあります。例えば、多重共線性の問題があります。これは、独立変数同士が強く相関している場合に起こります。多重共線性が存在すると、回帰係数の推定が不安定になり、分析結果の解釈が難しくなります。このような問題を避けるために、分析前に変数間の相関を確認し、必要に応じて変数を削除したり変更したりすることが重要です。Excelでは、相関係数を計算する機能も提供されているため、事前に多重共線性の確認を行うことができます。

独立変数と従属変数の指定

Excelで重回帰分析を行う際、独立変数と従属変数の指定は非常に重要なステップです。独立変数とは、分析の対象となる変数で、これらが従属変数にどのような影響を与えるかを調べます。従属変数は、独立変数の影響を受け、その変動を説明しようとする変数です。例えば、マーケティングの分析では、広告費や商品価格を独立変数とし、売上高を従属変数として分析することがよくあります。

独立変数と従属変数の指定は、Excelのデータ分析ツールパックを使用して行います。まず、データを適切に整形し、各列に独立変数と従属変数のデータを配置します。次に、データ分析ツールパックを起動し、重回帰分析のオプションを選択します。独立変数の範囲と従属変数の範囲を指定する欄に、それぞれのデータ範囲を入力します。この際、データの範囲を正確に指定することが重要です。範囲が正しくない場合、分析結果が予想通りにならなかったり、エラーが発生したりする可能性があります。

指定が完了したら、出力先を設定します。新しいワークシートや既存のワークシート内の指定したセルに結果を出力することができます。出力先を設定したら、分析を実行します。分析結果には、決定係数、回帰係数、p値などの重要な指標が含まれており、これらを用いて分析結果を解釈します。決定係数は、独立変数が従属変数の変動をどの程度説明しているかを示します。回帰係数は、各独立変数が従属変数に与える影響の大きさを示します。p値は、各独立変数が従属変数に有意な影響を与えているかどうかを判断する基準となります。

出力先の設定

出力先の設定は、重回帰分析の結果をどこに出力するかを指定する手順です。Excelでは、分析結果を新しいワークシートに表示させることも、既存のワークシートの特定のセルに直接出力することもできます。新しいワークシートを選択すると、分析結果が新たなシートに自動的に書き出され、既存のデータや計算式と干渉することなく確認できます。一方、特定のセルを選択すると、そのセルから始めて結果が表示されるため、分析結果と元のデータを並べて比較しやすくなります。出力先の設定は、分析結果の可視化や解釈のしやすさに大きく影響するため、適切な選択が重要です。

また、出力先の設定には、分析結果の整理や後処理の観点からも注意が必要です。例えば、新しいワークシートに結果を出力した場合、そのワークシートの名前を意味のあるものに変更しておくと、後での参照がしやすくなります。また、既存のワークシートに結果を出力する場合、出力先のセルが既に他のデータや式で使用されていないことを確認しましょう。これにより、分析結果が既存のデータに影響を与えることを防ぎ、正確な解釈が可能になります。出力先の設定は、分析の効率化と結果の信頼性向上に寄与します。

分析結果の確認と解釈

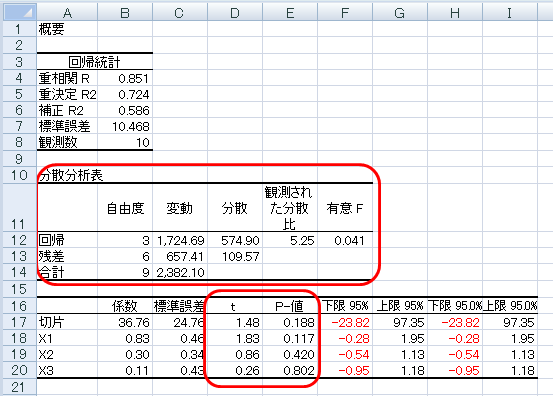
Excelの重回帰分析の結果を確認し、解釈することは、データの関係性を深く理解する上で重要なステップです。まず、決定係数（R^2）に注目します。決定係数は、従属変数の変動のうち、独立変数によって説明される割合を示します。R^2の値が1に近いほど、モデルの説明力が高くなることを意味します。例えば、R^2が0.85であれば、独立変数が従属変数の85%の変動を説明できているということです。

次に、回帰係数を確認します。回帰係数は、独立変数が1単位変化したときに、従属変数がどの程度変化するかを示します。正の回帰係数は、独立変数が増加すると従属変数も増加することを示し、負の回帰係数は逆の関係を示します。回帰係数の絶対値が大きいほど、その独立変数の影響力が大きいことを意味します。さらに、p値をチェックすることで、各独立変数が統計的に有意かどうかを判断します。p値が0.05未満であれば、その独立変数は従属変数に有意な影響があるとみなされます。

分析結果を解釈する際には、多重共線性の確認も重要です。多重共線性とは、独立変数の間に強い相関関係があることを指します。多重共線性がある場合、回帰係数の推定が不安定になり、結果の解釈が難しくなります。VIF（Variance Inflation Factor）値を計算することで、多重共線性の程度を評価できます。一般的に、VIF値が10以上になると、多重共線性の問題があるとされています。多重共線性を回避するためには、相関の高い変数を削除したり、変数を変換したりする方法があります。

Excelの重回帰分析は、マーケティングや金融などの分野で広く活用されています。例えば、マーケティングでは、広告費、価格、競合の活動などの独立変数を用いて、売上高の予測モデルを作成できます。金融では、金利、株価、経済指標などの独立変数を用いて、投資のリスクやリターンを分析することができます。これらの応用例を通じて、Excelの重回帰分析は、データに基づいた意思決定を支援する強力なツールとなっています。

決定係数の理解

決定係数は、重回帰分析において非常に重要な指標の一つです。これは、独立変数が従属変数の変動をどの程度説明しているかを表す数値で、0から1の範囲で示されます。決定係数が1に近いほど、独立変数が従属変数の変動をよく説明していることを意味し、0に近い場合は説明力が低いことを示します。したがって、決定係数はモデルの説明力を評価する上で重要な役割を果たします。

決定係数は、R²（R-squared）とも呼ばれ、モデルの適合度を定量的に示す指標です。例えば、R²が0.85の場合、独立変数が従属変数の変動の85%を説明していることを意味します。しかし、決定係数が高くても、モデルが必ずしも適切であるとは限りません。多重共線性や外れ値の存在など、他の要因も考慮する必要があります。したがって、決定係数はモデルの評価に役立つ一方で、他の統計量と組み合わせて使用することが推奨されます。

回帰係数とp値の解釈

回帰係数は、独立変数が1単位変化したときに、従属変数がどの程度変化するかを示す指標です。例えば、ある製品の販売数を予測するモデルで、広告費が1単位増加したときに、販売数が2単位増加するとする場合、広告費の回帰係数は2となります。回帰係数が正の値を示す場合、独立変数が増加すると従属変数も増加する傾向にあることを意味します。逆に、回帰係数が負の値を示す場合、独立変数が増加すると従属変数は減少する傾向にあることを示します。

p値は、独立変数が従属変数に実質的な影響を与えるかどうかを統計的に評価するための指標です。p値が0.05以下の場合、その独立変数が従属変数に有意な影響を及ぼしていると判断されます。つまり、その変数がモデルに重要な役割を果たしていることを示します。p値が0.05以上の場合、その独立変数が従属変数に影響を与えている証拠が十分でないことを意味します。このような場合、その変数をモデルから除外することを検討することもあります。

回帰係数とp値を組み合わせて解釈することで、各独立変数が従属変数にどのように影響しているかを具体的に理解することができます。例えば、ある独立変数の回帰係数が正でp値が0.05以下である場合、その変数は従属変数に有意に正の影響を与えていると判断できます。逆に、回帰係数が負でp値が0.05以下である場合、その変数は従属変数に有意に負の影響を与えていると解釈できます。これらの指標を活用することで、データの関係性をより深く理解し、意思決定に役立てることが可能となります。

多重共線性の確認

多重共線性の確認は、重回帰分析において重要なステップの一つです。これは、独立変数間の相関関係が高すぎることにより、分析結果が不安定になることを指します。多重共線性が存在すると、回帰係数の推定値が不確実になり、個々の変数の影響を正確に評価することが難しくなります。Excelでは、VIF（Variance Inflation Factor）や相関行列を使って多重共線性の確認を行うことができます。

VIFは、各独立変数が他の独立変数によってどれだけ説明されているかを示す指標です。一般的に、VIFの値が10以上になると多重共線性が疑われるため、注意が必要です。Excelのデータ分析ツールパックを使用して、相関行列を生成することもできます。相関行列では、各変数間の相関係数を確認し、0.8以上の高い相関を示す変数ペアに注意を払います。これらの方法を用いて、多重共線性の可能性を評価し、必要に応じて分析モデルを調整することで、より信頼性の高い結果を得ることができます。

重回帰分析の応用例

Excelの重回帰分析は、さまざまな分野で広く応用されています。例えば、マーケティングでは、広告費、価格、季節要因など、複数の変数が売上に与える影響を分析することで、効果的なマーケティング戦略を立案できます。また、金融分野では、株価の変動を利息率、経済指標、企業業績などの複数の要因で説明し、投資判断の根拠とすることができます。さらに、不動産業界では、物件の価格を面積、立地、築年数などの複数の要因で予測し、適正な価格設定や投資のリスク評価に活用されています。

これらの応用例は、重回帰分析が単なる統計的手法にとどまらず、実際のビジネスや研究に直接的な価値をもたらすことを示しています。例えば、マーケティング戦略の立案では、広告費や価格の最適化を通じて、売上の最大化を図ることができます。金融分野では、株価の変動要因を理解することで、市場の動向をより正確に把握し、リスクを最小限に抑えながらリターンを最大化する投資戦略を構築できます。不動産業界では、物件の価格を正確に予測することで、取引の透明性を高め、不動産市場の健全な発展に貢献できます。

Excelでの他の分析方法

Excelは、データ分析のための多様なツールを提供しており、重回帰分析はその中でも特に重要な位置を占めています。しかし、Excelには重回帰分析以外にも様々な分析方法が存在します。例えば、一元配置分散分析（ANOVA）は、複数の群の平均が統計的に有意に差があるかどうかを検定するのに役立ちます。また、t検定は、2つの群の平均値が統計的に有意に異なるかどうかを判定するための手法です。さらに、相関分析は、2つの変数間の関係性を測定するのに使用されます。これらの分析方法は、それぞれ異なる目的や状況に適しており、データの特性に応じて適切に選択することで、より深い洞察を得ることができます。

また、Excelのデータ分析アドインを使用することで、これらの分析を簡単に実行することができます。データ分析アドインは、Excelの標準機能に追加の統計分析機能を提供し、ユーザーが高度な分析を行うことを可能にします。例えば、回帰分析や分散分析は、このアドインを通じて簡単にアクセスできます。さらに、ピボットテーブルやグラフ機能も、データの可視化や要約に欠かせないツールとして活用できます。これらの機能を組み合わせることで、複雑なデータセットから有意義な情報を抽出し、意思決定の基盤として利用することが可能です。

重回帰分析の制限点

重回帰分析は、複数の独立変数が従属変数に与える影響を解析する強力なツールですが、その有効性はデータの質と分析者の解釈能力に大きく依存します。まず、データの質について考えると、分析結果の精度はデータの量と質に大きく影響されます。不足したデータや誤ったデータは、分析結果に誤差を生む可能性があります。また、データが偏っている場合、分析結果は現実の状況を正確に反映しないことがあります。

次に、多重共線性の問題があります。多重共線性とは、独立変数同士の間に強い相関関係があることを指します。この状態では、各独立変数が従属変数に与える影響を正確に特定することが難しくなります。Excelでは、VIF（Variable Inflation Factor）を用いて多重共線性を確認することができますが、高度な統計的な知識が必要となります。

さらに、モデルの複雑性も考慮する必要があります。独立変数の数が増えると、モデルは複雑になり、解釈が難しくなる可能性があります。また、過剰適合（overfitting）のリスクも高まり、分析結果が特定のデータセットに過度に適合し、新しいデータに対する予測性能が低下する可能性があります。このような問題を避けるためには、モデルのシンプルさと予測性能のバランスを取ることが重要です。

最後に、Excelのグラフ機能の制限も指摘する必要があります。Excelは、基本的なグラフ作成には適していますが、高度な可視化や複雑なモデルのグラフ化には限界があります。より高度な分析や可視化が必要な場合は、専門的な統計ソフトウェアの使用を検討することも一つの選択肢となります。

まとめ

Excel を使用した重回帰分析は、複数の変数間の関係性を深く理解するための強力なツールです。この分析方法は、データが持つ潜在的なパターンや傾向を明らかにし、予測モデルの構築に役立ちます。具体的には、独立変数と従属変数の関係を数式で表現し、その関係性の強さや有意性を評価します。本記事では、Excelを使用して重回帰分析を行う手順を詳細に解説します。

まず、分析に必要なデータをExcelのワークシートに入力します。次に、データ分析ツールを起動し、重回帰のオプションを選択します。独立変数と従属変数を適切に指定し、出力先を設定することで、分析結果が生成されます。生成された結果には、決定係数、回帰係数、p値などの重要な指標が含まれています。これらの指標を解釈することで、モデルの適切性や変数の影響度を判断できます。

また、多重共線性の確認方法も重要です。多重共線性があると、分析結果が不安定になる可能性があります。Excelでは、VIF（変数間の相関係数の逆数）を計算することで、多重共線性の有無を確認できます。さらに、マーケティングや金融などの実際の応用例を紹介することで、重回帰分析の実践的な活用方法を示します。

最後に、Excelのデータ分析ツール以外の方法も触れます。LINEST関数や回帰式を用いて重回帰分析を行う方法を解説し、Excelの限界やグラフの機能の活用についても言及します。これらの知識を活かすことで、読者はより高度なデータ分析を行うことが可能になります。

よくある質問

1. 重回帰分析とは何ですか？

重回帰分析は、複数の独立変数（説明変数）が1つの従属変数（目的変数）にどのように影響を与えるかを分析する統計的手法です。この方法は、複数の要因が結果に及ぼす影響を定量的に把握し、予測モデルを作成するために使用されます。例えば、住宅価格を予測する場合、家の広さ、立地、築年数など複数の要素が価格に影響を与えるため、それぞれの影響度を分析することで、より正確な予測モデルを作成することが可能になります。重回帰分析は、線形回帰分析の拡張版であり、単回帰分析では1つの独立変数しか考慮できませんが、重回帰分析では複数の独立変数を考慮できます。

2. Excelで重回帰分析を行う方法は？

Excelで重回帰分析を行うには、「データ分析」ツールを使用します。まず、Excelの「ファイル」メニューから「オプション」を選択し、「アドイン」タブで「分析ツールパック」を有効にします。その後、データを入力し、分析したい範囲を選択します。次に、「データ」タブから「データ分析」を選択し、表示されるメニューから「回帰」を選択します。ここで、Y変数の範囲（従属変数）とX変数の範囲（独立変数）を指定し、必要に応じて出力範囲やグラフの出力などのオプションを設定します。このプロセスを完了することで、Excelは重回帰分析の結果を出力し、各独立変数の影響度やモデルの適合度を示した回帰係数やR²値などを提供します。

3. 重回帰分析の結果を解釈する方法は？

重回帰分析の結果を解釈する際には、主に回帰係数、R²値（決定係数）、p値などの指標に注目します。回帰係数は、各独立変数が従属変数に与える影響の大きさと方向を示します。正の回帰係数は、独立変数が増加すると従属変数も増加することを意味し、負の回帰係数は逆の関係を示します。R²値は、モデルが従属変数の変動をどの程度説明できるかを示す指標で、0から1の間の値を取り、1に近いほどモデルの適合度が高いことを意味します。p値は、各独立変数が従属変数に統計的に有意な影響を与えるかどうかを示します。一般的に、p値が0.05未満であれば、その変数は有意であると判断されます。

4. 重回帰分析の結果を用いて予測を行う方法は？

重回帰分析の結果を用いて予測を行うには、まず分析の結果から得られた回帰方程式を使用します。回帰方程式は、以下のような形式で表されます：Y = a + b1X1 + b2X2 + ... + bnXn。ここで、Yは従属変数、aは切片、b1, b2, ..., bnは各独立変数の回帰係数、X1, X2, ..., Xnは独立変数です。具体的には、新しいデータの各独立変数の値をこの方程式に代入することで、従属変数の予測値を計算できます。例えば、住宅価格を予測する場合、新しい家の広さ、立地、築年数などの値を方程式に代入し、それらの値に基づいて予測価格を計算します。この方法により、複数の要因が組み合わさった結果を定量的に予測することが可能になります。

田中陽翔